THIEF Model

THIEF methodology uses a more detailed calculation than heat soak to estimate cable failures. It uses the cable’s dimension and thermal data to calculate the temperature inside the cable. Assuming the heat transfer on a cable is largely in the radial direction, it calculates the one-dimensional radial conductive heat transfer with the surface boundary conditions taken as the temperature or heat flux calculated by CFAST. Cable is damaged when the internal cable temperature, after thermal attenuation from the cable’s jacket, exceeds a specific threshold for thermoplastic or thermoset. This method is more realistic compared to the heat-soak method; however, it takes more computation time and data. The method is selected when the modeler provides the cable’s data in the FRI3D model. Results from the fire simulation are used to calculate heat conduction inside cables’ radial cross-sections. The surface temperature is used as the boundary condition to solve the following transient conductive heat transfer equation:

$$\rho c\frac{dT}{dt}=\frac{1}{r}\frac{d}{dr}k\ r\frac{dT}{dr}$$

Where $\rho$, $c$, and $k$ are effective density, specific heat, and thermal conductivity respectively. The equation is solved by the finite difference method. The cable’s radius R is divided into N uniformly spaced radial grids of length dr. A time step constraint dt is selected based on the value of dr as a criterion of numerical stability:

$$dt=\frac{c\rho\ dr^2}{2k}$$

The boundary condition for this solution is given by:

$$\rho c\frac{T_i^{n+1}-T_i^n}{dt}=\frac{2k}{\left(r_{i+1}+r_i\right)}\frac{1}{2\ dr}\left[r_i\frac{T_{i+1}^n-T_i^n}{dr}-r_{i-1}\frac{T_i^n-T_{i-1}^n}{dr}+r_i\frac{T_{i+1}^{n+1}-T_i^{n+1}}{dr}-r_{i-1}\frac{T_i^{n+1}-T_{i-1}^{n+1}}{dr}\right]$$

The boundary condition for this solution is given by:

$$k\frac{T_{N+1}^n-T_N^n}{dr}={\dot{q}}^n\left(t^n\right)$$

Where $\dot{q}}^n\left(t^n\right) $ is the net heat flux at the surface due to the heat convection with the surrounding gas as follows:

$${\dot{q}}^n\left(t^n\right)=\varepsilon\sigma\left(T_g\left(t^n\right)^4-\left(T_s^n\right)^4\right)+h\left(T_g\left(t^n\right)-T_s^n\right)$$

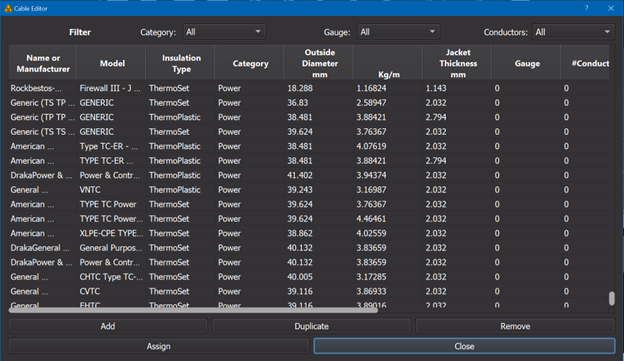
Where $\epsilon$ is the emissivity of the cable surface (assumed to be 0.95 in THIEF methodology), $\sigma$ is the Stefan-Boltzmann constant, $h$ is the convective heart transfer coefficient (assumed to be 10 $W/m^2/K$), and $T_g\left(t^n\right)$ is the effective gas temperature at the n-th time step. The effective gas temperature may be approximated by the cable’s surface temperature obtained from the preliminary CFAST simulation if the radial grid is reasonably small. The cable is assumed to fail when the internal cable temperature exceeds 400$\degree C$ and 200°C for thermoplastic and thermoset cables respectively. The failure timing is taken when that threshold is exceeded. To use the THIDF method, add a “Cable” in the model and select the cable material from the dropdown button or create a new one as shown in Figure 4 below.

What's next?